NERC  NERC NSS  This Home Page  ILRS
NERC Space Geodesy Facility
SPAD arming as a possible error source

The C-SPAD documentation states that the C-SPAD requires a 50ns settling down time after arming before meaningful data can be gathered.
This paper shows what can happen if you get track too soon after arming the C-SPAD using both Satellite and local calibration target data.
This paper also highlights how important it is to define your own system parameters and to apply them strictly during the reduction phase of observing. A list of parameters we apply at Herstmonceux are in the "Sources of Bias" page - coming soon

During a Starlette pass on Sept 28th the observer made a mistake and put in an offset which caused the track to get too close to the point that the C-SPAD was armed. After a minute or so he realised this and corrected the offset so that the track was greater than 50ns after arming the C-SPAD.

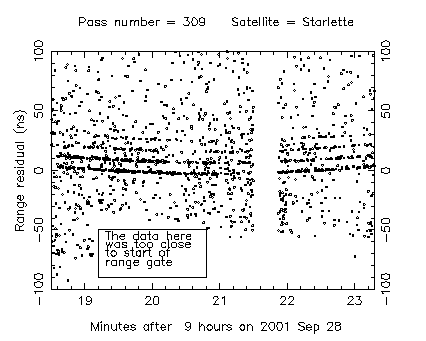
Figure 1. Expanded plot of the raw residuals for the whole pass showing the semi-train and noise. Outside minutes 19.2 and 21 noise can be seen greater than 50ns below the track. The gap in tha data during minute 22 is when the satellite went close to the Sun.

The pass looks quite normal and was reduced by our standard procedures. As part of our processing we insist that the final data set fit various constraints. This data set failed with a value for the Peak-LEHM (as derived from the Gaussian distribution process DISTRIB - SLRMAIL 0008) outside limits defined by the Herstmonceux system. As our system is strict the software will not let you send out data which fails any test. The observer must therefore find out why the data has failed.
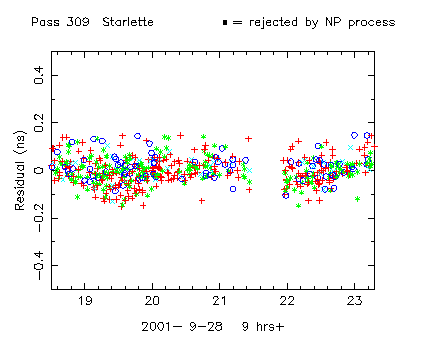
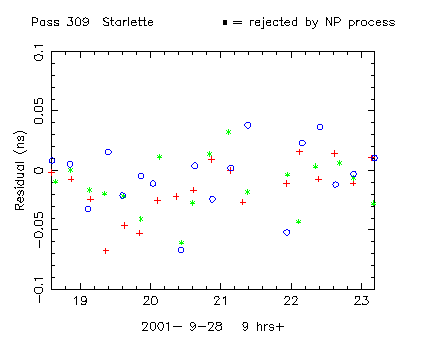
 Figure 2. Plot of the final residuals. The different coloured points represent the different pulses in the semi-train. There is a clear "bump" through minute 19

After some investigation it was realised that the observer had made a mistake during the observing. The pass was then re-reduced with all possible offending data removed.

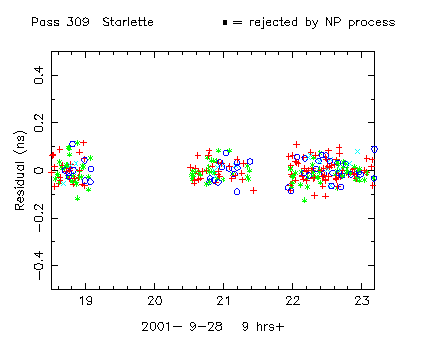
Figure 3. Final residuals with offending data missing. Note that the data for minute 23 has now come back in line.
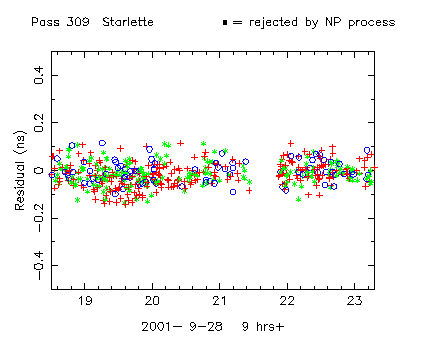
To complete the investigation we used the orbital solution obtained from the data shown in Fig. 3 and applied this solution to the full data set as shown below.
Figure 4a shows the final residuals for each individual point in the pass. Again the bulge during minute 19 can be seen, particularly for pulse 1 of the semi-train (red plus signs). The dip in the data is not as great for pulse 2(green) and there is no obvious dip for pulse 3(blue). This is what we would expect as pulses 2 and 3 are 9ns and 18ns further away from the arming point of the C-SPAD.

Figure 4b shows the mean values of the residuals for each pulse for each normal point bin.

From Figure 1 we can see that the C-SPAD was armed between 30ns and 50ns before the track for the erroneous data although the exact value is uncertain. The error values for the uncompensated channel obtained from calibrations as shown in Figure 5 for pre-arming values of 30ns-50ns agree closely to those shown in Figure 4b.

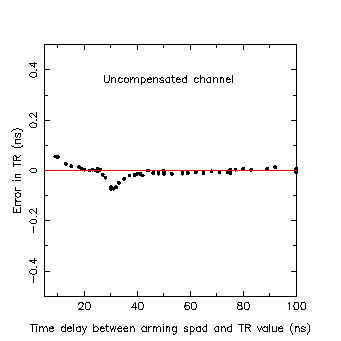
Arming Tests to Local Calibration Target


Figure 5
A series of local target observations were made each using different delays between the time of arming the C-SPAD and the calibration. The data for each calibration was then compared with a "control" calibration taken with a delay of 100ns between arming and data returns. To give us a fuller data set we used data from the first four pulses of our semi-train.
Figure 5 shows the results for the uncompensated channel of the C-SPAD.

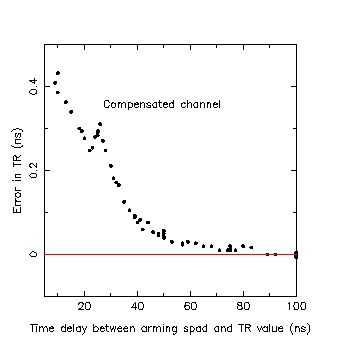
Figure 6
Figure 6 shows the results for the compensated channel of the C-SPAD.
It can be clearly seen that the behaviour of the compensated and uncompensated channels are considerably different and that much larger errors are introduced if you get too close to the arming point for the C-SPAD.